Explaining most of my assignments requires some preamble! Consider this tree:

   4   
 2   7
1 3 6 8

(I deliberately omitted 5; don’t worry about that for now.) You start at the root (4) and check if the thing you're looking for (say, 3) is equal to, less than, or greater than the thing you're looking at. If they're equal (you found it), hooray, we're done! If what you see is greater, you go down the left branch to look at things that are less – if it's less, you go down the right branch to look at things that are greater.

So in our example of looking for 3, we go left from 4, we go right from 2, and boom! there’s our 3.

That was the "nice" scenario. That tree was "balanced". Instead of explaining what a balanced tree is, let me show you an unbalanced tree, and you’ll get it right away:

1
 2
  3
   4
    6
     7
      8

See the difference? In the previous tree, everybody was only two steps from the root at most. Here, 8 is six steps from the root! But you're going to get a tree like this second example if someone feeds you a list of sorted numbers and asks you to make a tree out of it: 2 is greater than 1, 1 has no right child, so put 2 down the right side of 1... 3 is greater than 1, 3 is greater than 2, 2 has no right child, so put 3 down the right side of 2... you can see how you'd end up with a vine instead of a tree! (We care about this because we want to be able to make large trees that perform acceptably, and all these extra search steps take time.)

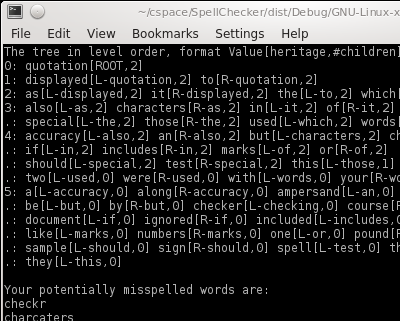
Now imagine if this was a much bigger tree, full of dictionary words in alphabetical order. Our job was to create this tree and somehow make it so that it was balanced (for this, I used my own hackneyed implementation of the Day-Stout-Warren algorithm).

We then processed a text file and displayed the misspelled words – anything that wasn't in the dictionary. You know that something isn't in the tree at all if you fall out of the tree instead of finding the thing: someone searching for 5 in the numeric examples would just hit the dead end trying to go left from the node holding 6.

A bubble sort is very easy to code – if you are sure that you are only ever going to have a handful of items, go ahead and write one. It's not a bad place to start learning.

But a bubble sort generally takes time proportional to the square of the items you have to sort. As you can imagine, that gets out of hand in a hurry. What you want is an algorithm that tends to sort in time proportional to, say, the number of items you have to sort times its logarithm. That's not nearly as bad.

We tend to develop programs using "tiny toy data sets", and it's easy to write something that provides perfectly acceptable performance in the testing environment but performs abysmally poorly when subject to real-world tests. Read more here: Everything is Fast for Small n.

So for our assignment, we generated a list of 10,000 random integers. We implemented various sorting algorithms and timed the results. You can see this in the "Sorting" project in the download.

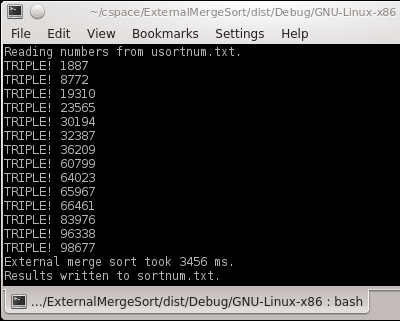
But the real pièce de résistance was the external merge sort. So you have your file with 10,000 numbers. What if you only can store 1,000 numbers in memory at a time?

What you do is you load the file in 10 runs of 1,000 numbers – at the end of each run, sort the numbers (with a mergesort if you need stability), and save them somewhere else.*

So now you have 10 files with 10 sorted lists. Your task now is to merge them. You can set up 10 file readers and one output file writer. Start by having every file writer load their first number. Take the "left lowest" number, and write it to the output file. Then move the corresponding file reader to the next line. Repeat. You can see this in the "ExternalMergeSort" in the download – I used 10 file readers on two buffer files instead of 10 buffer files, but it's the same idea. (We might as well have used one file, but the assignment requirements were fairly prescriptive.)

* - With my program, if 1,000 really was a hard limit, I'd have to do 20 runs of 500 or something, because my mergesort is not "in-place" – it needs extra memory to work with. A quicksort can be done in-place, but is not stable – number n from line a won’t necessarily slot in before the same number n from line a-plus-something.